Cylindrical
Cavity Field Equations for Stationary and Spinning Modes
This analysis
of the cylindrical cavity is based on that for the spherical cavity.
The
procedure used is very similar to that in 'Spherical Cavity Field
Equations' which should be consulted
for details
of the analysis as this page mainly contains just the results. The
general form
of the well known field equations for a cylindrical cavity normal
stationary
resonant modes are as follows:-
Cylindrical
Stationary H Wave
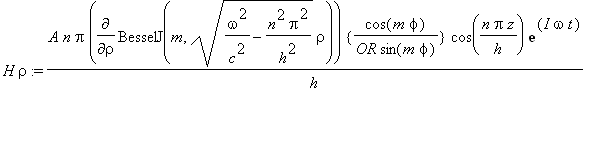........(1a)
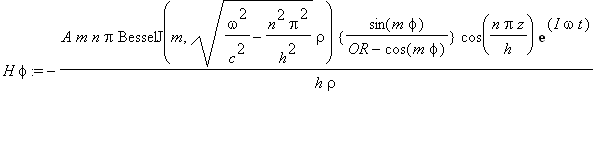......(1b)
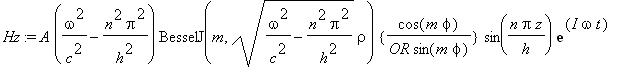......(1c)
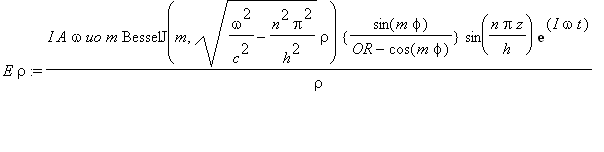......(1d)
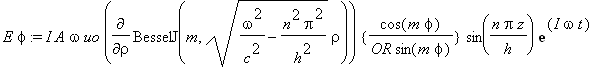...(1e)
...............(1f)
Cylindrical
Stationary E Wave
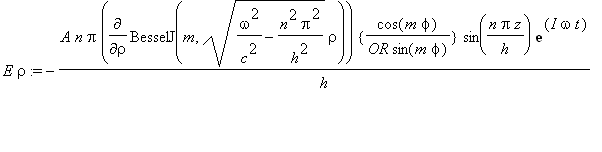.......(2a)
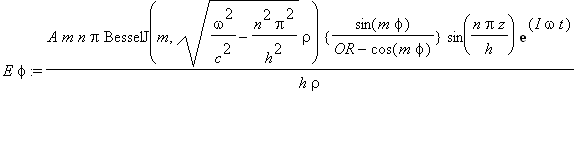.......(2b)
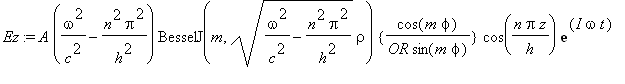......(2c)
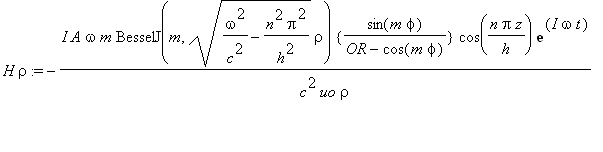......(2d)
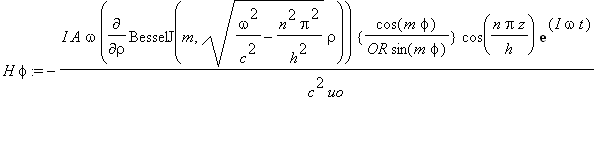.....(2e)
................(2f)
NOTES ON
EQUATIONS:-
1. The symbols
used in the equations are as follows:-
m,n -- Can take
the value 0, 1, 2, 3.....etc and are the integers defining the harmonic
solutions. (Sometimes called the eigenvalues)
c -- The
velocity of light
A -- An
arbitrary constant which determines the amplitude of all the field
components.
, z -- The usual
cylindrical coordinates
ie 
is
the radius of the cylindrical cavity, 
is the rotational
angle about the z axis measured anticlockwise
from the x axis, and z is the usual z axis along which the cylinder
height is
measured.
t -- Time
h --The height
of the cylindrical field.
-- The resonant
angular frequency in radians per second (
)
2. The meaning
of terms such as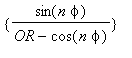 
is
that either the top term is used for each field component or the bottom
term is
used. For a particular resonant mode it is not permissible to mix terms
from
the top and bottom for the E and H fields. The minus sign included with
the
bottom term indicates that this field component is multiplied by -1.
Although
the equations look different if the top terms are used instead of the
bottom
the only effect is that the bottom terms represent rotation of all the
fields
clockwise, in the direction of 
, by 
radians
(90 degrees) electrical. Because all field
components are rotated together no new field configuration is normally
produced. However, if m = 0 then sin(m 
) = 0 and cos(m
) = 1 so the top terms produce a valid field
whereas the
bottom terms do not. It is therefore generally preferable to use the
top terms
rather than the bottom. .
3. The term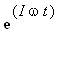 
represents
a rotating vector of
magnitude one and rotating at a frequency 
. For the usual
stationary fields of a standard cavity
resonator it represents the sinusoidally varying amplitude with time.
The H
fields have a term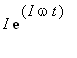 
and the 
term
represent a phase advance in time of the sinusoidal H
field on the E field by 
radians.
4. The above
equations define a field which has zero divergence of both electric and
magnetic fields and satisfy Maxwell’s equations for a field in vacuum,
without charges or currents, of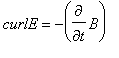 
and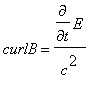 
.
5. The
differential of the BesselJ expression is:-
= 
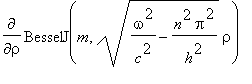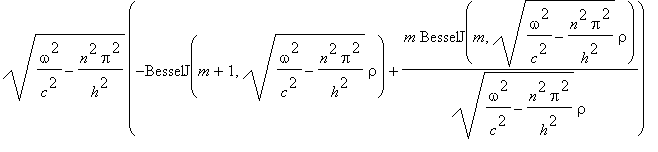
Re-writting
The Spinning Field Equations.
The above
equations and notes represent the standard interpretation of the fields
in a
resonant cylindrical cavity. However, in the same way as was shown for
the
spherical cavity the cylindrical cavity equations can also describe a
spinning
field .The changes which can be made to the equations to more readily
be seen
to represent a spinning field are as follows:-
1. We can
compare the rate of change of the above fields with time by
differentiating
with respect to t and comparing this with the rate of change due to
spin by
multiplying by 
and differentiating with
respect to 
. We
again find that the two rates of change are identical and this
therefore means
that the spinning and stationary cylindrical fields themselves have
identical
field distributions. We do still get a minus sign for the spinning
fields rate
of change showing that the spinning fields are just rotated 
radians
(180 degrees) electrical
with respect to the stationary fields.
2. The 
term now
refers to the field change that
occurs due to the field spinning in space with constant amplitude about
the z
axis in the direction of 
. 
would
be the frequency of the field as sensed by a probe positioned so as to
measure
the frequency of the field rotating past it. This can be considered as
the
electrical speed of rotation and the mechanical frequency of spin ( 
) will be 
radians per second.
This
follows because there are m cycles of the field in each revolution in
the 
direction. In fact it is because
the field is sinusoidal in the 
direction that
rotation in this direction is to the
observer the same as a field variation in time. If m = 0 then there is
no
variation of the field in the 
direction so no
field variation with rotation and therefore
this is not a possible spinning mode. All higher values of m ie 1,2,3,4
etc
will produce spinning fields. For the spinning field instead of using 
which refers to the electrical
variation we can, if preferred, replace all occurrences of it by 
m which is still the
electrical variation but expressed in terms of the mechanical spin
frequency.
Therefore 
becomes 
etc.
3. The 
term in the E field
equations 1d and 1e and the H field
equations 2d and 2e above referred to a time phase difference between
fields.
It now refers to a space phase difference which requires that the H
field is
rotated 
electrical
in space relative to the E field. This is 
radians of
mechanical rotation. This
phase difference is essential for the fields to spin but can be
expressed in a
different way by removing the I term using the following equations
which apply
to rotating fields unless m = 0. As already stated m = 0 is not a valid
spinning mode so the substitution is valid-
= 
= 
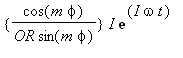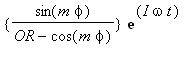
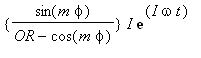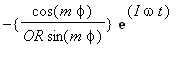
4 The
exponential terms such as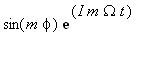 
represent rotation in the 
direction
and can be written as the equivalent expression 
. You can see
this later expression also represents rotation as for t=0 say then at 
= 0 the
field will be zero.
However, as t increases 
must increase to
keep 
equal to zero
and the increasing value 
with time is
rotation.
Making these
four changes to eqn (1) we have the following field equations for a
spinning
field:-
Cylindrical
Spinning H Wave
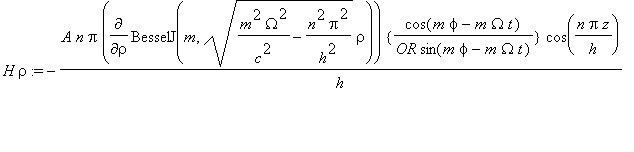........(3a)
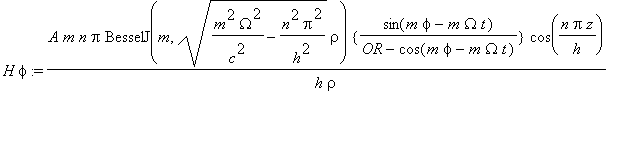......(3b)
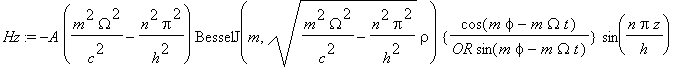......(3c)
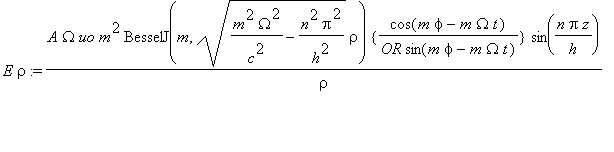......(3d)
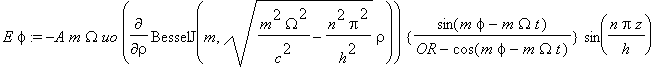...(3e)
...............(3f)
Cylindrical
Spinning E Wave
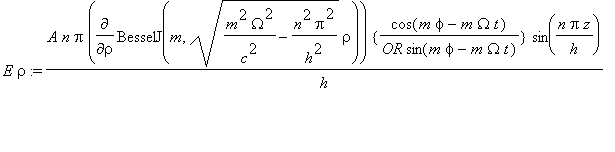.......(4a)
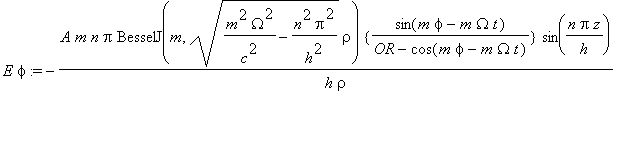.......(4b)
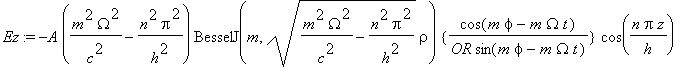......(4c)
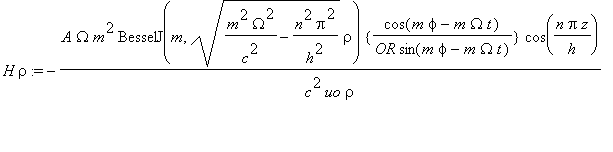......(4d)
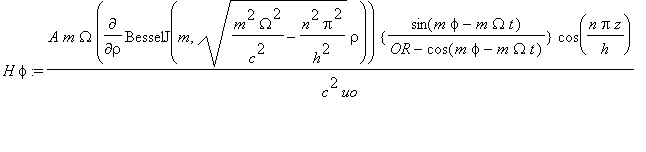.....(4e)
................(4f)
NOTES ON
EQUATIONS:-
m,n -- m can
take the value 1, 2, 3.....etc and n can take the values 0, 1, 2,
3....etc.
--the mechanical
rotational angular frequency.
In order to
confirm that the field equations have been correctly manipulated it is
only
necessary to check that the E and H fields in equations (3) and (4)
satisfy
Maxwell's equations. For this it is necessary to use the full equations
with
either the top or bottom 
term. This has
been done using a computer program written in Maple 6 and the equations
comply
with all four of Maxwell's equations.