TABLES
OF LOWEST CYLINDRICAL
CAVITY RESONANT MODES
Properties
of H Wave Modes:-
For resonance BesselJ(m+1, R) – 
x BesselJ(m,
R) = 0 where
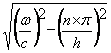
Resonant
frequency (f Hz) =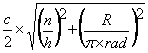 
where
R and n have the values in the table below.
Rotational angular frequency (Ω radians/sec) = 
=
Phase velocity = Ω rad.
|
STATIONARY AND SPINNING MODES |
SPINNING MODE ONLY |
||||||
|
MODE |
For 83.4 cm diameter, 50 cm high cavity oscillating in first radial mode
|
||||||
|
m (ф term) |
Radial Harmonics(R) |
n (z term) |
Resonant Frequency (MHz) |
Rotational Speed (106rev/sec) |
Phase Velocity2 |
||
|
1 |
2 |
3 |
|||||
|
0 |
Not Allowed |
0 |
-- |
Not Allowed |
|||
|
0 |
3.83 |
7.02 |
10.17 |
1 |
531.3 |
Not Allowed |
|
|
1 |
Not Allowed |
0 |
-- |
Not Allowed |
|||
|
1 |
1.84 |
5.331 |
8.54 |
1 |
366.6 |
366.6 |
3.20c |
|
1 |
1.84 |
5.33 |
8.54 |
2 |
635.9 |
635.9 |
5.55c |
|
1 |
1.84 |
5.33 |
8.54 |
3 |
924.3 |
924.3 |
8.07c |
|
2 |
Not Allowed |
0 |
-- |
Not Allowed |
|||
|
2 |
3.05 |
6.71 |
9.97 |
1 |
460.4 |
230.2 |
2.01c |
|
2 |
3.05 |
6.71 |
9.97 |
2 |
694.2 |
347.1 |
3.03c |
|
2 |
3.05 |
6.71 |
9.97 |
3 |
965.4 |
482.7 |
4.22c |
Properties
of E Wave Modes:-
For resonance BesselJ(m, R) = 0 where
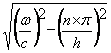
Resonant frequency (f Hz) = 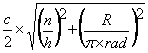where
R and n have the values in the table below.
Rotational angular frequency (Ω radians/sec) = =
Phase velocity = Ω rad
|
STATIONARY AND SPINNING MODES |
SPINNING MODE ONLY |
||||||
|
MODE |
For 83.4 cm diameter, 50 cm high cavity oscillating in first radial mode
|
||||||
|
m (ф term) |
Radial Harmonics(R) |
n (z term) |
Resonant Frequency (MHz) |
Rotational Speed (106rev/sec) |
Phase Velocity2 |
||
|
1 |
2 |
3 |
|||||
|
0 |
2.40 |
5.52 |
8.65 |
0 |
274.8 |
Not Allowed |
|
|
0 |
2.40 |
5.52 |
8.65 |
1 |
406.8 |
Not Allowed |
|
|
1 |
3.83 |
7.02 |
10.17 |
0 |
438.5 |
438.5 |
3.83c |
|
1 |
3.83 |
7.02 |
10.17 |
1 |
531.3 |
531.3 |
4.64c |
|
1 |
3.83 |
7.02 |
10.17 |
2 |
743.2 |
743.2 |
6.49c |
|
1 |
3.83 |
7.02 |
10.17 |
3 |
1001.1 |
1001.1 |
8.74c |
|
2 |
5.14 |
8.42 |
11.62 |
0 |
588.5 |
294.2 |
2.57c |
|
2 |
5.14 |
8.42 |
11.62 |
1 |
660.6 |
330.3 |
2.88c |
|
2 |
5.14 |
8.42 |
11.62 |
2 |
840.4 |
420.2 |
3.67c |
|
2 |
5.14 |
8.42 |
11.62 |
3 |
1075.3 |
537.6 |
4.70c |
GENERAL
NOTES:-
1 This mode is TE121 (i.e. Derived
from the numbers in the m column, the R column heading and the n
column). 5.33
is the second value of R that makes the BesselJ
function zero.
2 Unlike the spherical cavity, where
the phase velocity depends only on the mode, in the cylindrical cavity
it also
depends on the cavity size.
3.
The symbols used above are as follows:-
m,n
-Can take the values 0, 1,
2, 3……etc and are the integers defining the harmonic
solutions.
(Sometimes called the eigenvalues)
c
-The velocity of light.
ω –The
resonant angular frequency
Ω -
The rotational angular frequency.
f
-The
resonant
frequency.
(Where f = 
) . For
the spinning
field this will be the frequency measured by a probe and will be 
.
h
-The height of the cylindrical cavity.
rad -The radius
of the cylindrical cavity.
φ -The
coordinate measuring the angle of rotation about the z axis measured
from
the
x axis (in the initial direction of the y axis)